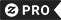Golden Spiral and Fibonacci Spiral T-Shirt

The Golden Spiral (back design) is constructed by repeatedly dividing Golden Rectangles in half. A rectangle with proportions such that when divided in half (parallel to a short side) each half has the same proportions, is a Golden Rectangle, and the ratio of a long side to a short side is the Golden Ratio (1.61803398874989484820458683436564). To make a Golden Spiral, divide a Golden Rectangle in half, then divide one of the halves in half, and repeat as long as you like. Which half is divided next is chosen so that diagonals can be drawn across successively smaller rectangles so that these diagonals form a spiral. The Fibonacci Spiral (front design) is constructed by diagonals across squares. The sizes of the squares are determined by the Fibonacci series 1, 1, 2, 3, 5, 8, 13, 21.. where each integer is the sum of the two previous integers. Instead of constructing the spiral from the outside in as for the Golden Spiral, we construct this spiral from the inside out. We start with two squares of size 1 (the length of a side). We can place one square against the other neatly because the sides have the same length. Two other sides are colinear (lie on one line) with a combined length of 2. We place a square of size 2 against this combined length. Then we place diagonals on the three squares such that the diagonals lie end-to-end, making the beginning of the spiral. Now we find two colinear sides of lengths 1 and 2 that touch the longest diagonal, and we place a square of size 3 against this combined length and add another diagonal to the spiral. As we repeat this procedure, we graphically produce the Fibonacci series. The Fibonacci series is related to the Golden Ratio because ratios of adjacent values of the Fibonacci series are increasingly better approximations of the Golden Ratio: 21/13=1.6153, 34/21=1.6190, 55/34=1.6176, etc.